Change of basis vs linear transformation
31 May 2016There are two related concepts in linear algebra that may seem confusing at first glance: change of basis and linear transformation. Change of basis formula relates coordinates of one and the same vector in two different bases, whereas a linear transformation relates coordinates of two different vectors in the same basis. The difficulty in discerning these two cases stems from the fact that the word vector is often misleadingly used to mean coordinates of a vector. Generally speaking, $\newcommand{\vec}{\mathbf} \vec{x} \neq (x_1, x_2)^T$, unless a certain basis is understood.
Change of basis
Let’s consider a concrete example. Let $(\vec{u}_1, \vec{u}_2)$ be an orthonormal basis in $\mathbb{R}^2$. Imagine we make a copy of it $(\vec{v}_1, \vec{v}_2)$ and rotate the copy by $\theta$ degrees.
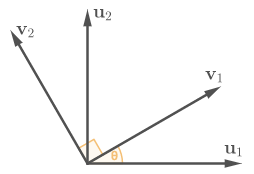
Rotation of the basis vectors by angle $\theta$.
Without loss of generality, we can identify the initial basis vectors with the standard unit vectors of $\mathbb{R}^2$:
Now, vectors $\vec{v}_1$ and $\vec{v}_2$ can be easily represented in the basis $(\vec{u}_1, \vec{u}_2)$ as
More compactly, one writes
The rotation matrix on the right-hand side relates bases $(\vec{u}_1, \vec{u}_2)$ and $(\vec{v}_1, \vec{v}_2)$. In general, change of basis in $\mathbb{R}^2$ is described by the formula
where $(\vec{u}_1, \vec{u}_2)$ is an old basis, $(\vec{v}_1, \vec{v}_2)$ is a new basis, and matrix $(\vec{u} \to \vec{v})$ specifies a relationship between them.
Change of coordinates of a vector
A vector is an object that exists independent of a basis. Although it is common in engineering and mathematics to write $\vec{x} = (x_1, x_2)^T$, one should be aware that this notation implies a certain choice of a basis; namely, it implies that the standard basis of $\mathbb{R}^2$ is chosen. That is,
with $(\vec{u}_1, \vec{u}_2)$ from \eqref{standard_basis}.
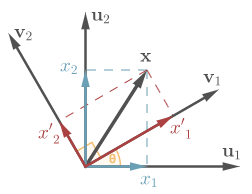
Expansion of vector $\vec{x}$ in two bases.
Let’s consider coordinates of $\vec{x}$ in basis $(\vec{v}_1, \vec{v}_2)$. Analogously to \eqref{vec_in_u},
Equating expansions of $\vec{x}$ \eqref{vec_in_u} and \eqref{vec_in_v} while substituting \eqref{change_of_basis} in place of $(\vec{v}_1, \vec{v}_2)$, we obtain
On both sides, we have expansions of $\vec{x}$ in basis $(\vec{u}_1, \vec{u}_2)$, therefore coordinates on both sides should be equal. Thus, we arrive at the formula for the change of coordinates of a vector under change of basis
whith coordinates of $\vec{x}$ in the old basis $\vec{x}^\vec{u} = (x_1, x_2)^T$, and coordinates of $\vec{x}$ in the new basis $\vec{x}^\vec{v} = (x’_1, x’_2)^T$.
Linear transformation
In contrast to the previous section, we now fix the basis $(\vec{u}_1, \vec{u}_2)$ and represent all vectors in that basis. The question we want to answer is “How to represent a linear transformation $\newcommand{\bphi}{\boldsymbol{\phi}} \bphi : \mathbb{R}^2 \to \mathbb{R}^2$ by a matrix?”
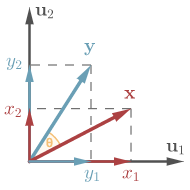
Vector $\vec{x}$ is rotated by angle $\theta$.
Let’s apply $\bphi$ to some vector $\vec{x}$:
By expanding $\vec{y}$ in basis $(\vec{u}_1, \vec{u}_2)$ and rewriting the right-hand side as matrix-vector multiplication, we obtain
Now we are approaching the point where confusion arises. Assume $\bphi$ rotates every vector by $\theta$. Then the matrix representation of $\bphi$ is precisely the matrix $(\vec{u} \to \vec{v})$ we had before. Therefore,
where we identify vectors with their coordinates in the standard basis as conventionally done in sciences (i.e., $\vec{y} = \vec{y}^\vec{u}$ and $\vec{x} = \vec{x}^\vec{u}$).
Compare formulas \eqref{change_of_coordinates} and \eqref{linear_transformation}. They look very similar as they both relate two column vectors via the same matrix. There is, however, a big difference between them. Equation \eqref{change_of_coordinates} expresses the coordinates of $\vec{x}$ in the old reference frame given its coordinates in the new one, whereas equation \eqref{linear_transformation} expresses the coordinates of the transformed vector $\vec{x}$ given the coordinates of the untransformed vector $\vec{x}$—all in one reference frame. We could also invert \eqref{change_of_coordinates} to always have new coordinates on the left-hand side, $\vec{x}^\vec{v} = (\vec{u} \to \vec{v})^{-1} \vec{x}^\vec{u}$. In this form, the meaning of the difference between \eqref{change_of_coordinates} and \eqref{linear_transformation} becomes clear.
The best strategy to avoid mistakes is to pick one of the two possibilities—either transform bases or transform vectors—and stick with it.
How transformations transform
Let’s have a look at how linear transformations transform under a change of basis. Notation in this section slightly differs from the rest of the article; namely, we use primed symbols to denote objects related to a new basis.
Consider a basis transformation $\vec{u} = \vec{u}’ \vec{T}^{-1}$, where $\vec{u}$ is the old basis and $\vec{u}’$ is the new basis. Then,
or, in tensor notation,